アーク溶接 第54話 溶接電流・アーク電圧(1) 担当 高木柳平
2016年06月06日
◆はじめに
本話からしばらく「個別溶接条件の選定」について説明します。
第6話、第48話のなかで「アーク溶接の主要10大条件」を示しましたが、溶接条件ではとりわけ溶接電流、アーク電圧、溶接速度の3条件が重要であり、そのわけはビード形状、溶け込み深さをほぼ決定するためです。まず、「溶接電流」の説明から始めます。
溶接電流には瞬時電流などの動的電流と平均電流などの静的電流がありますが、ここでは平均電流I(A)で話を進めます。溶接アークと言う負荷はオームの法則に従い、例えば200A-24Vであればその抵抗Rは以下の公式により0.12Ωとなります。
![]() ここでI;溶接電流(A) V;アーク電圧(V) R;抵抗(Ω)
ここでI;溶接電流(A) V;アーク電圧(V) R;抵抗(Ω)
アークはほぼ0.1Ω前後の抵抗値を有する負荷と考えれば良く、周りの状況(接触給電抵抗、磁気、ガス圧力など)によってばらつきやすく、純粋な電気抵抗と比べると不安定負荷と言えそうです。オームの法則はアーク溶接を理解する上で大変役立ちますので、今後ともその都度活用することをお勧めします。ここで直流溶接電源をアークと言う負荷に接続した模式図を図054-01に示す。
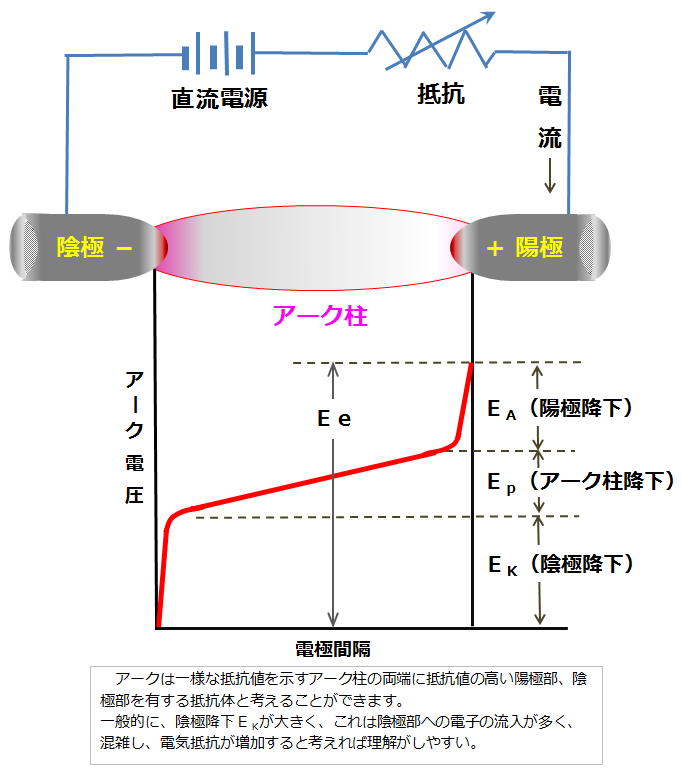
この図は一般的にアークの電位分布を説明するために用いられますが、図から陰極と陽極およびそれらの近傍で急激な電圧降下があることが読み取れます。すなわち両極部とその近傍では抵抗が高くなっていることを示しています。アークは一様な抵抗値を示すアーク柱の両端に抵抗値の高い陽極部、陰極部を有する抵抗体と考えることができます。
一方、実際のアークの場合の模式図を図054-02に示します。
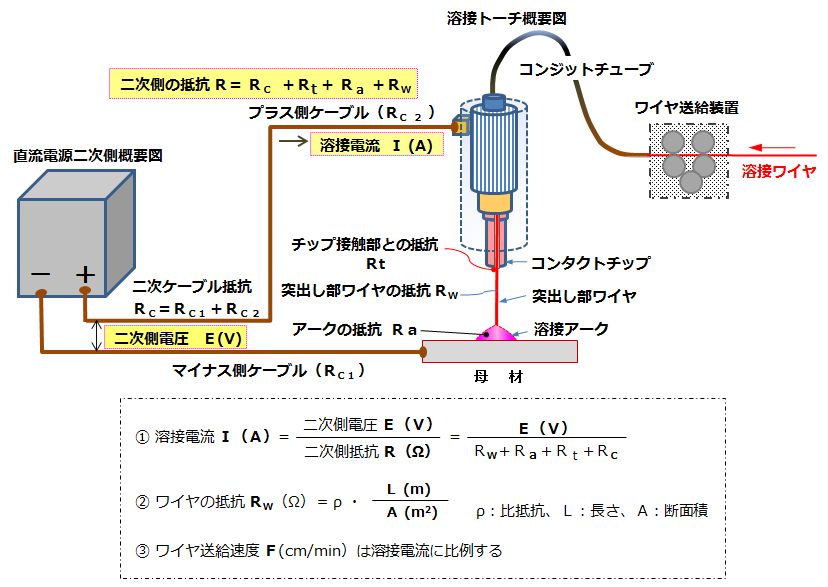
溶接電源直流側のプラス側ケーブルはトーチ・コンタクトチップに、マイナス側ケーブルは母材に接続され、この場合のアークからみた外部抵抗Rは二次側ケーブルの抵抗Rc、チップ孔との接触抵抗Rtおよび突出し長さ部分のワイヤ抵抗Rwの総和です。アークの抵抗をRaとし、溶接電源の二次側電圧をE(V)とすると溶接電流I(A)は次式で表すことができる。
![]()
これよりわかることは、E(V)は設定電圧のためほぼ一定であり、抵抗を構成するなかでもRa、Rt、Rcなどの変動は少ないがRwは突出し長さの変動により溶接電流I(A)値に大きな影響を与える。細部をみればRtのチップとの接触抵抗の変動と同時に接触位置の変動がRwのバラツキにもなる。
ここでワイヤの抵抗値Rwについてみてみましょう。第11話でも説明しましたがRwは以下の式で表すことができます。
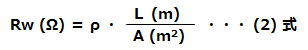
ここでρは比抵抗(Ω・m)、Aはワイヤの断面積(m2)、Lはワイヤ長さ(m)を示す。以上から溶接電流の値は設定電圧E(V)を一定とするとワイヤによる抵抗値に反比例の関係にあり、次のように表現できる。
①ワイヤの長さL(m)は突出し長さと関係しLが長ければ電流が減少し、短ければ増加する。
突き出し長さ部は溶接電流Iが流れることによってI2 × Rw熱が発生し加熱されワイヤ保有熱量が増加する。ワイヤの比抵抗ρ(Ω・m)は温度と相関があり、温度上昇とともに増加する。よって突き出し長さが長くなればRwが大となりI2 × Rw熱によりさらに多く発熱し比抵抗ρが増加しRwを大きくすると言う関係になります。
②ワイヤ断面積A(m2)はワイヤ径を表しAが大きければRwが減少し、電流が増加、小さければRwが増加し、電流が減少する。
ワイヤ送り速度F(cm/min)を一定とするとΦ1.2のワイヤはΦ0.9ワイヤより大きな電流が流れることになる。逆に言えば薄板溶接で小さい電流が 必要な時は、Φ0.9ワイヤはΦ1.2に比べ小電流域で適用範囲が広く、都合がよくなります。一方、突出し長さ(ここではL)、ワイヤ径(ここではA)を 一定としワイヤ送給速度F(m/min)とすると溶接電流I(A)とは正比例の関係を示します。すなわちFを速くするとIは増加し、Fを遅くするとIは減少します。この関係は溶接条件設定には大変重要です。そのわけは、単位時間当たりのワイヤ送給量がa倍になったと仮定すると(2)式Aにa×Aを代入すればRwは1/aとなり(1)式より溶接電流はa×Iとなることから容易に理解することができます。
次回は溶接電流とワイヤ径、ワイヤ送給速度の関係について基本的な考え方を説明します。
以上。
